[0001] '@'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q - t}{q {\left(t - 1\right)}^{2}}\)
Graph:
1 vertex: [0]
0 edges: []

[0002] 'A?'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{2} t + q^{2} - 4 \, q t + t^{2} + t}{q^{2} {\left(t - 1\right)}^{3}}\)
Graph:
2 vertices: [0, 1]
0 edges: []

[0003] 'A_'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{2} - t}{q^{2} {\left(t - 1\right)}^{2}}\)
Graph:
2 vertices: [0, 1]
1 edge: [[0, 1]]

[0004] 'B?'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{3} t^{2} + 4 \, q^{3} t - 6 \, q^{2} t^{2} + q^{3} - 12 \, q^{2} t + 12 \, q t^{2} - t^{3} + 6 \, q t - 4 \, t^{2} - t}{q^{3} {\left(t - 1\right)}^{4}}\)
Graph:
3 vertices: [0, 1, 2]
0 edges: []

[0005] 'BG'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{3} t + q^{3} - 2 \, q^{2} t - 2 \, q t + t^{2} + t}{q^{3} {\left(t - 1\right)}^{3}}\)
Graph:
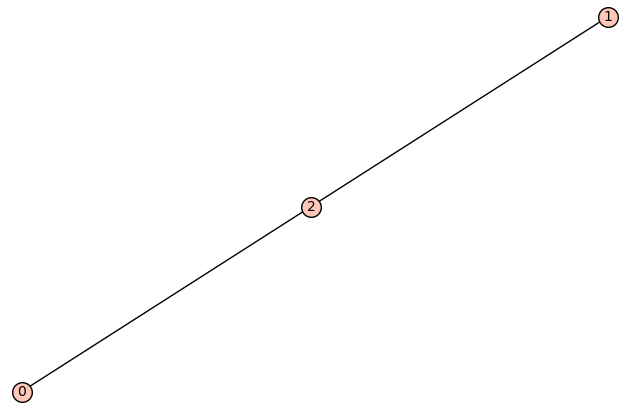
3 vertices: [0, 1, 2]
1 edge: [[1, 2]]

[0006] 'BW'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{4} + q^{3} t - 4 \, q^{2} t + q t + t^{2}}{{\left(q - t\right)} q^{3} {\left(t - 1\right)}^{2}}\)
Graph:
3 vertices: [0, 1, 2]
2 edges: [[0, 2], [1, 2]]

[0007] 'Bw'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{3} - t}{q^{3} {\left(t - 1\right)}^{2}}\)
Graph:
3 vertices: [0, 1, 2]
3 edges: [[0, 1], [0, 2], [1, 2]]

[0008] 'C?'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{4} t^{3} + 11 \, q^{4} t^{2} - 8 \, q^{3} t^{3} + 11 \, q^{4} t - 56 \, q^{3} t^{2} + 24 \, q^{2} t^{3} + q^{4} - 32 \, q^{3} t + 96 \, q^{2} t^{2} - 32 \, q t^{3} + t^{4} + 24 \, q^{2} t - 56 \, q t^{2} + 11 \, t^{3} - 8 \, q t + 11 \, t^{2} + t}{q^{4} {\left(t - 1\right)}^{5}}\)
Graph:
4 vertices: [0, 1, 2, 3]
0 edges: []

[0009] 'C@'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{4} t^{2} + 4 \, q^{4} t - 4 \, q^{3} t^{2} + q^{4} - 8 \, q^{3} t + 2 \, q^{2} t^{2} - 2 \, q^{2} t + 8 \, q t^{2} - t^{3} + 4 \, q t - 4 \, t^{2} - t}{q^{4} {\left(t - 1\right)}^{4}}\)
Graph:
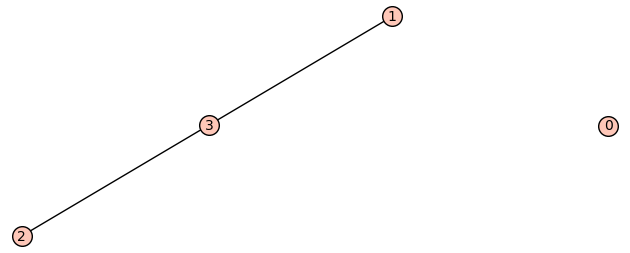
4 vertices: [0, 1, 2, 3]
1 edge: [[2, 3]]

[0010] 'CB'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{6} t - 2 \, q^{5} t^{2} - q^{4} t^{3} + q^{6} + q^{4} t^{2} + 6 \, q^{3} t^{3} - 10 \, q^{4} t + 8 \, q^{3} t^{2} - 10 \, q^{2} t^{3} + 6 \, q^{3} t + q^{2} t^{2} + t^{4} - q^{2} t - 2 \, q t^{2} + t^{3}}{{\left(q - t\right)}^{2} q^{4} {\left(t - 1\right)}^{3}}\)
Graph:
4 vertices: [0, 1, 2, 3]
2 edges: [[1, 3], [2, 3]]

[0011] 'CF'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{6} + 4 \, q^{5} t + q^{4} t^{2} - 12 \, q^{4} t - 6 \, q^{3} t^{2} + 6 \, q^{3} t + 12 \, q^{2} t^{2} - q^{2} t - 4 \, q t^{2} - t^{3}}{{\left(q - t\right)}^{2} q^{4} {\left(t - 1\right)}^{2}}\)
Graph:
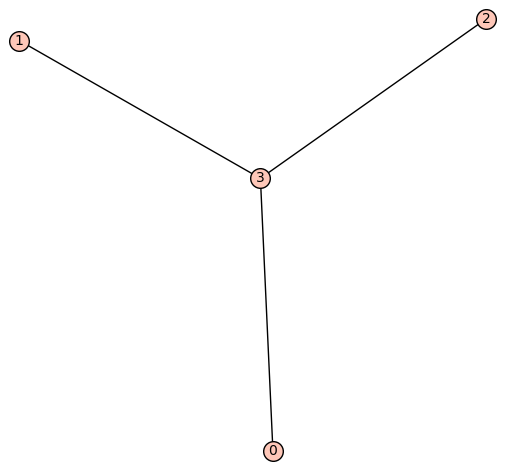
4 vertices: [0, 1, 2, 3]
3 edges: [[0, 3], [1, 3], [2, 3]]

[0012] 'CJ'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{4} t + q^{4} - 2 \, q^{3} t - 2 \, q t + t^{2} + t}{q^{4} {\left(t - 1\right)}^{3}}\)
Graph:
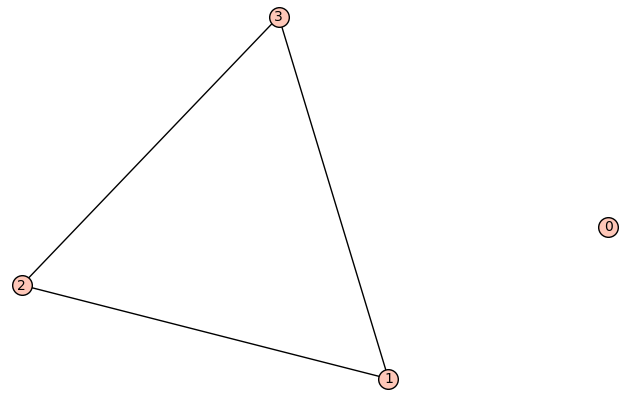
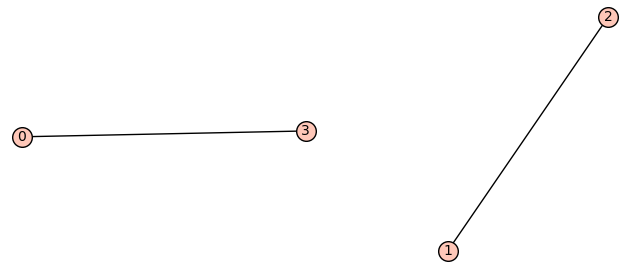
4 vertices: [0, 1, 2, 3]
3 edges: [[1, 2], [1, 3], [2, 3]]

[0013] 'CK'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{4} t + q^{4} - 4 \, q^{2} t + t^{2} + t}{q^{4} {\left(t - 1\right)}^{3}}\)
Graph:
4 vertices: [0, 1, 2, 3]
2 edges: [[0, 3], [1, 2]]

[0014] 'CL'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{6} + 2 \, q^{5} t - q^{4} t^{2} - 6 \, q^{4} t + 6 \, q^{2} t^{2} + q^{2} t - 2 \, q t^{2} - t^{3}}{{\left(q - t\right)}^{2} q^{4} {\left(t - 1\right)}^{2}}\)
Graph:
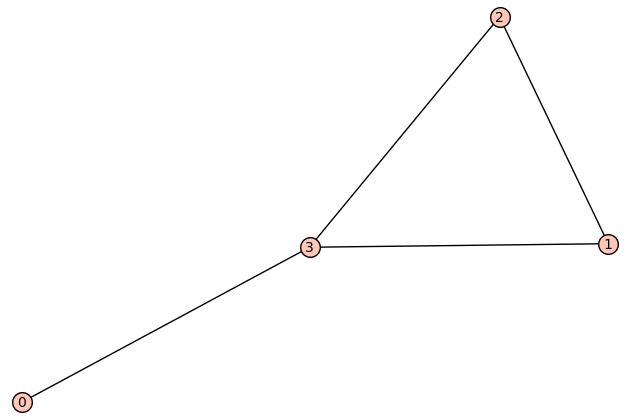
4 vertices: [0, 1, 2, 3]
3 edges: [[0, 3], [1, 2], [2, 3]]

[0015] 'CN'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{5} + q^{4} t - 2 \, q^{3} t - 2 \, q^{2} t + q t + t^{2}}{{\left(q - t\right)} q^{4} {\left(t - 1\right)}^{2}}\)
Graph:
4 vertices: [0, 1, 2, 3]
4 edges: [[0, 3], [1, 2], [1, 3], [2, 3]]

[0016] 'C]'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{6} + 3 \, q^{4} t - 8 \, q^{3} t + 3 \, q^{2} t + t^{2}}{{\left(q^{2} - t\right)} q^{4} {\left(t - 1\right)}^{2}}\)
Graph:
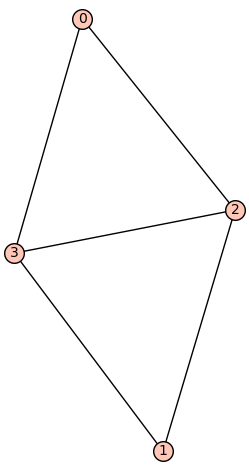
4 vertices: [0, 1, 2, 3]
4 edges: [[0, 2], [0, 3], [1, 2], [1, 3]]

[0017] 'C^'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{6} + q^{4} t - 4 \, q^{3} t + q^{2} t + t^{2}}{{\left(q^{2} - t\right)} q^{4} {\left(t - 1\right)}^{2}}\)
Graph:
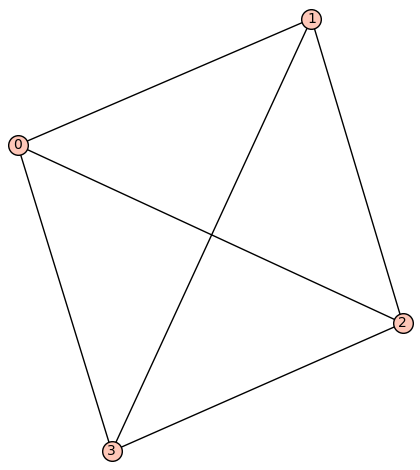
4 vertices: [0, 1, 2, 3]
5 edges: [[0, 2], [0, 3], [1, 2], [1, 3], [2, 3]]

[0018] 'C~'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{4} - t}{q^{4} {\left(t - 1\right)}^{2}}\)
Graph:
4 vertices: [0, 1, 2, 3]
6 edges: [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]]

[0019] 'D??'

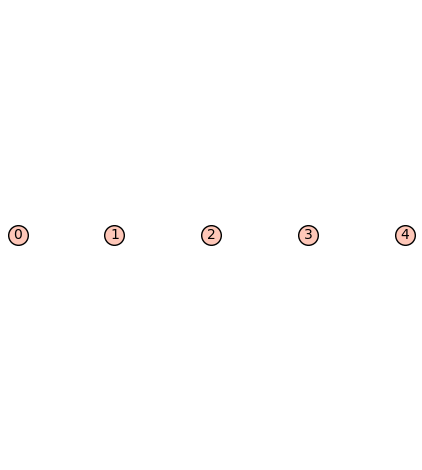
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{5} t^{4} + 26 \, q^{5} t^{3} - 10 \, q^{4} t^{4} + 66 \, q^{5} t^{2} - 180 \, q^{4} t^{3} + 40 \, q^{3} t^{4} + 26 \, q^{5} t - 330 \, q^{4} t^{2} + 480 \, q^{3} t^{3} - 80 \, q^{2} t^{4} + q^{5} - 80 \, q^{4} t + 600 \, q^{3} t^{2} - 600 \, q^{2} t^{3} + 80 \, q t^{4} - t^{5} + 80 \, q^{3} t - 480 \, q^{2} t^{2} + 330 \, q t^{3} - 26 \, t^{4} - 40 \, q^{2} t + 180 \, q t^{2} - 66 \, t^{3} + 10 \, q t - 26 \, t^{2} - t}{q^{5} {\left(t - 1\right)}^{6}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
0 edges: []

[0020] 'D?C'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{5} t^{3} + 11 \, q^{5} t^{2} - 6 \, q^{4} t^{3} + 11 \, q^{5} t - 42 \, q^{4} t^{2} + 10 \, q^{3} t^{3} + q^{5} - 24 \, q^{4} t + 34 \, q^{3} t^{2} + 4 \, q^{2} t^{3} + 4 \, q^{3} t + 34 \, q^{2} t^{2} - 24 \, q t^{3} + t^{4} + 10 \, q^{2} t - 42 \, q t^{2} + 11 \, t^{3} - 6 \, q t + 11 \, t^{2} + t}{q^{5} {\left(t - 1\right)}^{5}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
1 edge: [[3, 4]]

[0021] 'D?K'

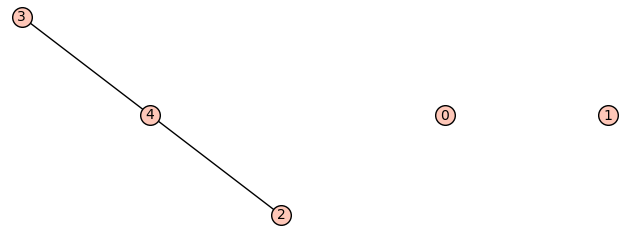
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{8} t^{2} - 3 \, q^{7} t^{3} + 5 \, q^{6} t^{4} + q^{5} t^{5} + 4 \, q^{8} t - 12 \, q^{7} t^{2} + 4 \, q^{6} t^{3} - 12 \, q^{5} t^{4} - 8 \, q^{4} t^{5} + q^{8} - 3 \, q^{7} t + q^{6} t^{2} + 55 \, q^{5} t^{3} - 16 \, q^{4} t^{4} + 22 \, q^{3} t^{5} - 22 \, q^{6} t + 48 \, q^{5} t^{2} - 132 \, q^{4} t^{3} + 48 \, q^{3} t^{4} - 22 \, q^{2} t^{5} + 22 \, q^{5} t - 16 \, q^{4} t^{2} + 55 \, q^{3} t^{3} + q^{2} t^{4} - 3 \, q t^{5} + t^{6} - 8 \, q^{4} t - 12 \, q^{3} t^{2} + 4 \, q^{2} t^{3} - 12 \, q t^{4} + 4 \, t^{5} + q^{3} t + 5 \, q^{2} t^{2} - 3 \, q t^{3} + t^{4}}{{\left(q - t\right)}^{3} q^{5} {\left(t - 1\right)}^{4}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
2 edges: [[2, 4], [3, 4]]

[0022] 'D?['

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{8} t - 3 \, q^{7} t^{2} - 9 \, q^{6} t^{3} - q^{5} t^{4} + q^{8} + 7 \, q^{7} t + 3 \, q^{6} t^{2} + 41 \, q^{5} t^{3} + 8 \, q^{4} t^{4} - 30 \, q^{6} t - 12 \, q^{5} t^{2} - 54 \, q^{4} t^{3} - 24 \, q^{3} t^{4} + 24 \, q^{5} t + 54 \, q^{4} t^{2} + 12 \, q^{3} t^{3} + 30 \, q^{2} t^{4} - 8 \, q^{4} t - 41 \, q^{3} t^{2} - 3 \, q^{2} t^{3} - 7 \, q t^{4} - t^{5} + q^{3} t + 9 \, q^{2} t^{2} + 3 \, q t^{3} - t^{4}}{{\left(q - t\right)}^{3} q^{5} {\left(t - 1\right)}^{3}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
3 edges: [[1, 4], [2, 4], [3, 4]]

[0023] 'D?{'

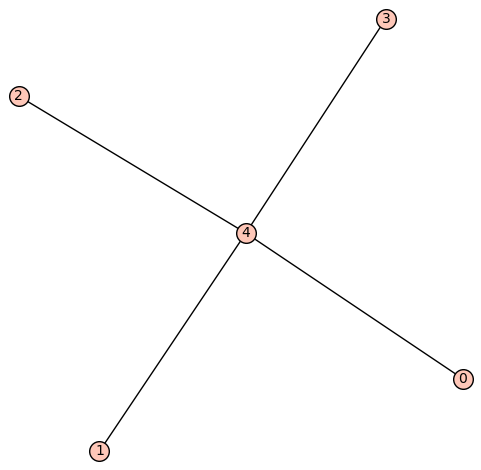
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{8} + 11 \, q^{7} t + 11 \, q^{6} t^{2} + q^{5} t^{3} - 32 \, q^{6} t - 56 \, q^{5} t^{2} - 8 \, q^{4} t^{3} + 24 \, q^{5} t + 96 \, q^{4} t^{2} + 24 \, q^{3} t^{3} - 8 \, q^{4} t - 56 \, q^{3} t^{2} - 32 \, q^{2} t^{3} + q^{3} t + 11 \, q^{2} t^{2} + 11 \, q t^{3} + t^{4}}{{\left(q - t\right)}^{3} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
4 edges: [[0, 4], [1, 4], [2, 4], [3, 4]]

[0024] 'D@K'

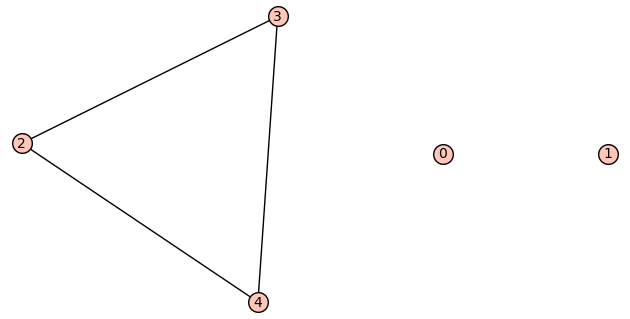
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{5} t^{2} + 4 \, q^{5} t - 4 \, q^{4} t^{2} + q^{5} - 8 \, q^{4} t + 4 \, q^{3} t^{2} + 2 \, q^{3} t - 2 \, q^{2} t^{2} - 4 \, q^{2} t + 8 \, q t^{2} - t^{3} + 4 \, q t - 4 \, t^{2} - t}{q^{5} {\left(t - 1\right)}^{4}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
3 edges: [[2, 3], [2, 4], [3, 4]]

[0025] 'D@O'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{5} t^{2} + 4 \, q^{5} t - 2 \, q^{4} t^{2} + q^{5} - 4 \, q^{4} t - 4 \, q^{3} t^{2} - 8 \, q^{3} t + 8 \, q^{2} t^{2} + 4 \, q^{2} t + 4 \, q t^{2} - t^{3} + 2 \, q t - 4 \, t^{2} - t}{q^{5} {\left(t - 1\right)}^{4}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
2 edges: [[1, 4], [2, 3]]

[0026] 'D@S'

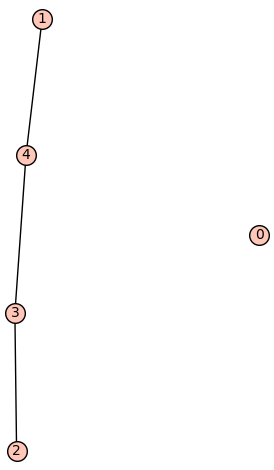
Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{8} t - 3 \, q^{7} t^{2} - 3 \, q^{6} t^{3} + q^{5} t^{4} + q^{8} + 3 \, q^{7} t - q^{6} t^{2} + 19 \, q^{5} t^{3} - 2 \, q^{4} t^{4} - 16 \, q^{6} t + 6 \, q^{5} t^{2} - 24 \, q^{4} t^{3} - 6 \, q^{3} t^{4} + 6 \, q^{5} t + 24 \, q^{4} t^{2} - 6 \, q^{3} t^{3} + 16 \, q^{2} t^{4} + 2 \, q^{4} t - 19 \, q^{3} t^{2} + q^{2} t^{3} - 3 \, q t^{4} - t^{5} - q^{3} t + 3 \, q^{2} t^{2} + 3 \, q t^{3} - t^{4}}{{\left(q - t\right)}^{3} q^{5} {\left(t - 1\right)}^{3}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
3 edges: [[1, 4], [2, 3], [3, 4]]

[0027] 'D@['

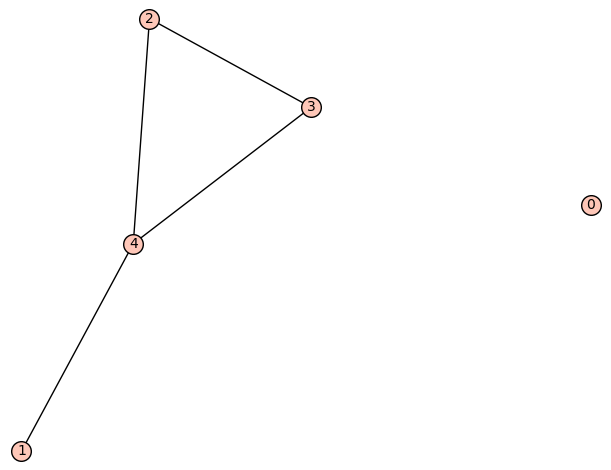
Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{7} t - 2 \, q^{6} t^{2} - q^{5} t^{3} + q^{7} + q^{5} t^{2} + 4 \, q^{4} t^{3} - 6 \, q^{5} t + 4 \, q^{4} t^{2} - 2 \, q^{3} t^{3} - 2 \, q^{4} t + 4 \, q^{3} t^{2} - 6 \, q^{2} t^{3} + 4 \, q^{3} t + q^{2} t^{2} + t^{4} - q^{2} t - 2 \, q t^{2} + t^{3}}{{\left(q - t\right)}^{2} q^{5} {\left(t - 1\right)}^{3}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
4 edges: [[1, 4], [2, 3], [2, 4], [3, 4]]

[0028] 'D@s'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{8} + 5 \, q^{7} t - q^{6} t^{2} - q^{5} t^{3} - 12 \, q^{6} t - 8 \, q^{5} t^{2} + 4 \, q^{4} t^{3} + 24 \, q^{4} t^{2} + 4 \, q^{4} t - 8 \, q^{3} t^{2} - 12 \, q^{2} t^{3} - q^{3} t - q^{2} t^{2} + 5 \, q t^{3} + t^{4}}{{\left(q - t\right)}^{3} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
4 edges: [[0, 4], [1, 4], [2, 3], [3, 4]]

[0029] 'D@{'

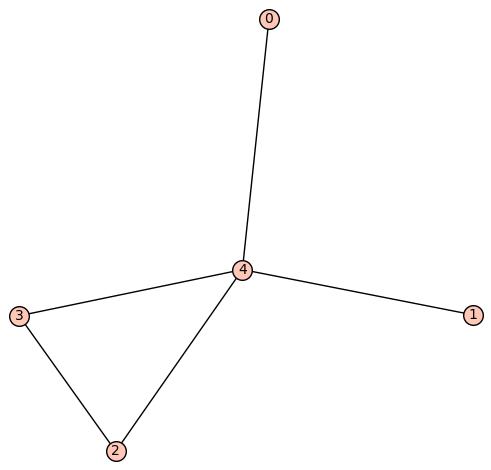
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{7} + 4 \, q^{6} t + q^{5} t^{2} - 8 \, q^{5} t - 4 \, q^{4} t^{2} - 2 \, q^{4} t + 2 \, q^{3} t^{2} + 4 \, q^{3} t + 8 \, q^{2} t^{2} - q^{2} t - 4 \, q t^{2} - t^{3}}{{\left(q - t\right)}^{2} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
5 edges: [[0, 4], [1, 4], [2, 3], [2, 4], [3, 4]]

[0030] 'DBW'

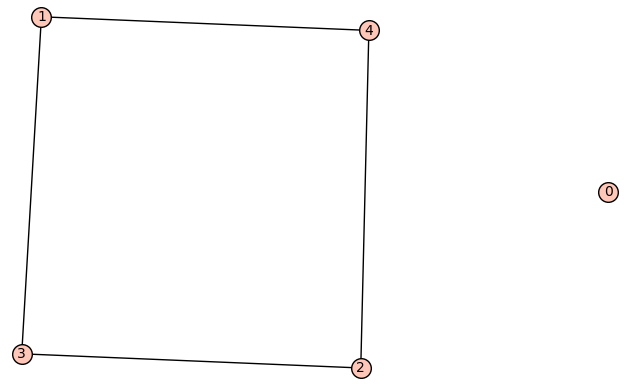
Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{9} t + q^{9} - 2 \, q^{8} t - 2 \, q^{7} t^{2} + 6 \, q^{7} t - 3 \, q^{5} t^{3} - 20 \, q^{6} t + 5 \, q^{5} t^{2} + 14 \, q^{4} t^{3} + 14 \, q^{5} t + 5 \, q^{4} t^{2} - 20 \, q^{3} t^{3} - 3 \, q^{4} t + 6 \, q^{2} t^{3} - 2 \, q^{2} t^{2} - 2 \, q t^{3} + t^{4} + t^{3}}{{\left(q^{2} - t\right)}^{2} q^{5} {\left(t - 1\right)}^{3}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
4 edges: [[1, 3], [1, 4], [2, 3], [2, 4]]

[0031] 'DB['

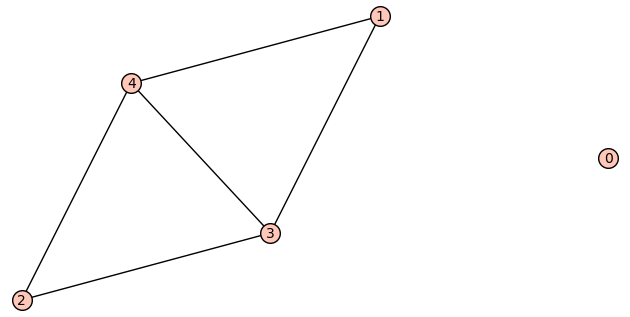
Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{9} t + q^{9} - 2 \, q^{8} t - 2 \, q^{7} t^{2} + 2 \, q^{7} t + 2 \, q^{6} t^{2} - q^{5} t^{3} - 10 \, q^{6} t + 3 \, q^{5} t^{2} + 6 \, q^{4} t^{3} + 6 \, q^{5} t + 3 \, q^{4} t^{2} - 10 \, q^{3} t^{3} - q^{4} t + 2 \, q^{3} t^{2} + 2 \, q^{2} t^{3} - 2 \, q^{2} t^{2} - 2 \, q t^{3} + t^{4} + t^{3}}{{\left(q^{2} - t\right)}^{2} q^{5} {\left(t - 1\right)}^{3}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
5 edges: [[1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

[0032] 'DBg'

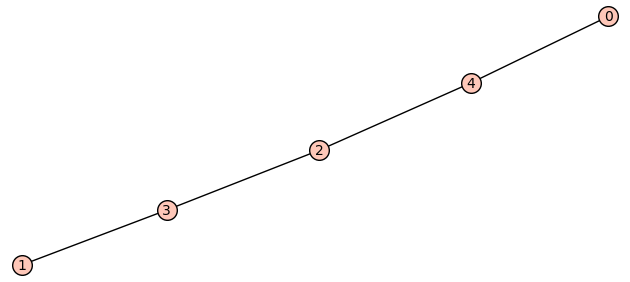
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{10} + 3 \, q^{9} t - 3 \, q^{8} t^{2} + q^{7} t^{3} - 7 \, q^{8} t - 5 \, q^{7} t^{2} + q^{6} t^{3} + q^{5} t^{4} - 6 \, q^{7} t + 26 \, q^{6} t^{2} + 6 \, q^{5} t^{3} - 6 \, q^{4} t^{4} + 6 \, q^{6} t - 6 \, q^{5} t^{2} - 26 \, q^{4} t^{3} + 6 \, q^{3} t^{4} - q^{5} t - q^{4} t^{2} + 5 \, q^{3} t^{3} + 7 \, q^{2} t^{4} - q^{3} t^{2} + 3 \, q^{2} t^{3} - 3 \, q t^{4} - t^{5}}{{\left(q^{2} - t\right)} {\left(q - t\right)}^{3} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
4 edges: [[0, 4], [1, 3], [2, 3], [2, 4]]

[0033] 'DBk'

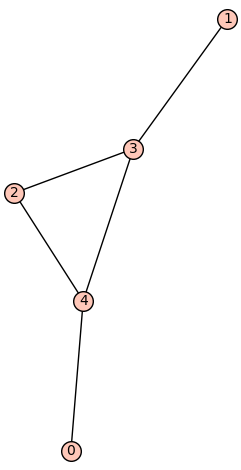
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{9} + 2 \, q^{8} t - q^{7} t^{2} - 3 \, q^{7} t - 2 \, q^{6} t^{2} - q^{5} t^{3} - 8 \, q^{6} t + 6 \, q^{5} t^{2} + 6 \, q^{4} t^{3} + 6 \, q^{5} t + 6 \, q^{4} t^{2} - 8 \, q^{3} t^{3} - q^{4} t - 2 \, q^{3} t^{2} - 3 \, q^{2} t^{3} - q^{2} t^{2} + 2 \, q t^{3} + t^{4}}{{\left(q^{2} - t\right)} {\left(q - t\right)}^{2} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
5 edges: [[0, 4], [1, 3], [2, 3], [2, 4], [3, 4]]

[0034] 'DB{'

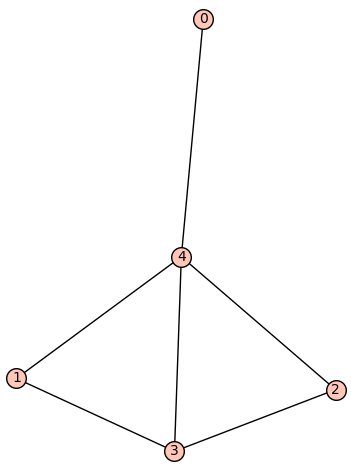
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{10} + q^{9} t - 2 \, q^{7} t^{2} - 10 \, q^{7} t + q^{6} t^{2} - q^{5} t^{3} + 6 \, q^{6} t + 8 \, q^{5} t^{2} + 6 \, q^{4} t^{3} - q^{5} t + q^{4} t^{2} - 10 \, q^{3} t^{3} - 2 \, q^{3} t^{2} + q t^{3} + t^{4}}{{\left(q^{2} - t\right)}^{2} {\left(q - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
6 edges: [[0, 4], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

[0035] 'DFw'

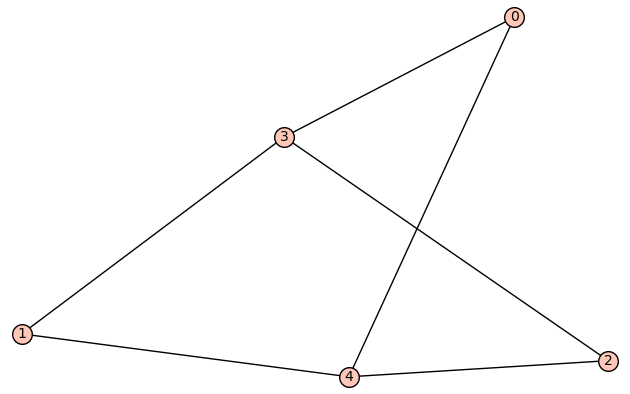
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{12} + 4 \, q^{10} t - 11 \, q^{9} t + q^{8} t^{2} + 2 \, q^{8} t - 14 \, q^{7} t^{2} + q^{7} t + 32 \, q^{6} t^{2} + q^{5} t^{3} - 14 \, q^{5} t^{2} + 2 \, q^{4} t^{3} + q^{4} t^{2} - 11 \, q^{3} t^{3} + 4 \, q^{2} t^{3} + t^{4}}{{\left(q^{3} - t\right)} {\left(q^{2} - t\right)}^{2} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
6 edges: [[0, 3], [0, 4], [1, 3], [1, 4], [2, 3], [2, 4]]

[0036] 'DF{'

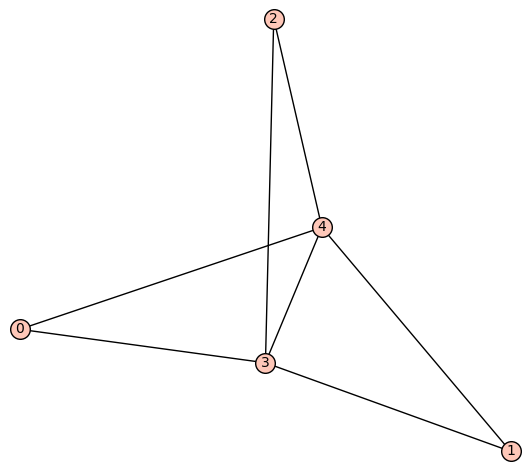
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{9} + 4 \, q^{7} t - 12 \, q^{6} t + q^{5} t^{2} + 6 \, q^{5} t - 6 \, q^{4} t^{2} - q^{4} t + 12 \, q^{3} t^{2} - 4 \, q^{2} t^{2} - t^{3}}{{\left(q^{2} - t\right)}^{2} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
7 edges: [[0, 3], [0, 4], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

[0037] 'DIk'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{10} + q^{9} t + 2 \, q^{8} t - 2 \, q^{7} t^{2} - 14 \, q^{7} t - 3 \, q^{6} t^{2} - q^{5} t^{3} + 8 \, q^{6} t + 16 \, q^{5} t^{2} + 8 \, q^{4} t^{3} - q^{5} t - 3 \, q^{4} t^{2} - 14 \, q^{3} t^{3} - 2 \, q^{3} t^{2} + 2 \, q^{2} t^{3} + q t^{3} + t^{4}}{{\left(q^{2} - t\right)}^{2} {\left(q - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
5 edges: [[0, 4], [1, 2], [1, 3], [2, 4], [3, 4]]

[0038] 'DJ['

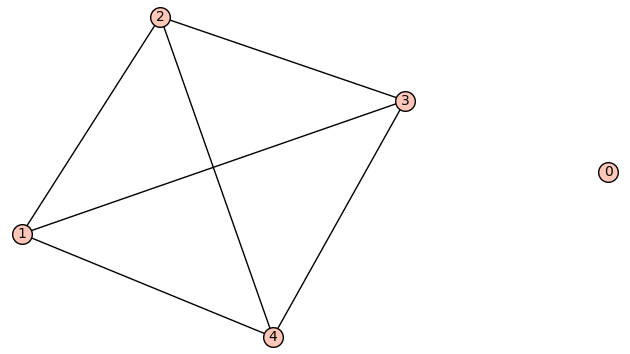
Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{5} t + q^{5} - 2 \, q^{4} t - 2 \, q t + t^{2} + t}{q^{5} {\left(t - 1\right)}^{3}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
6 edges: [[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

[0039] 'DJk'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{6} + q^{5} t - 4 \, q^{3} t + q t + t^{2}}{{\left(q - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
6 edges: [[0, 4], [1, 2], [1, 3], [2, 3], [2, 4], [3, 4]]

[0040] 'DJ{'

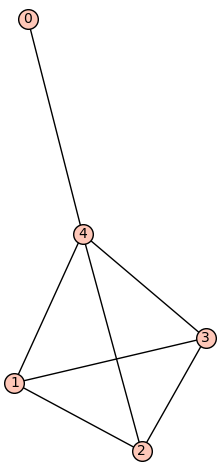
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{6} + q^{5} t - 2 \, q^{4} t - 2 \, q^{2} t + q t + t^{2}}{{\left(q - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
7 edges: [[0, 4], [1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

[0041] 'DK['

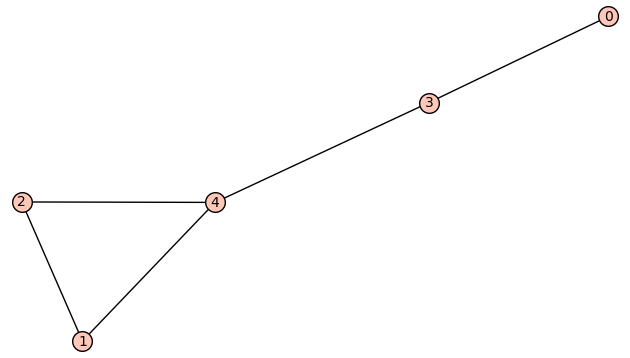
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{7} + 2 \, q^{6} t - q^{5} t^{2} - 4 \, q^{5} t - 2 \, q^{4} t + 2 \, q^{3} t^{2} + 4 \, q^{2} t^{2} + q^{2} t - 2 \, q t^{2} - t^{3}}{{\left(q - t\right)}^{2} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
5 edges: [[0, 3], [1, 2], [1, 4], [2, 4], [3, 4]]

[0042] 'DK{'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{6} + q^{5} t - 4 \, q^{3} t + q t + t^{2}}{{\left(q - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
6 edges: [[0, 3], [0, 4], [1, 2], [1, 4], [2, 4], [3, 4]]

[0043] 'DLo'

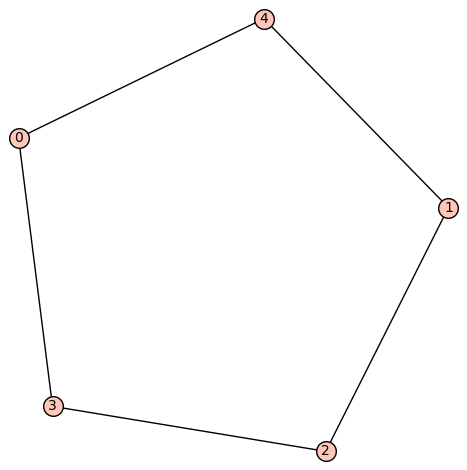
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{9} + 8 \, q^{7} t - 20 \, q^{6} t + q^{5} t^{2} + 10 \, q^{5} t - 10 \, q^{4} t^{2} - q^{4} t + 20 \, q^{3} t^{2} - 8 \, q^{2} t^{2} - t^{3}}{{\left(q^{2} - t\right)}^{2} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
5 edges: [[0, 3], [0, 4], [1, 2], [1, 4], [2, 3]]

[0044] 'DL{'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{9} + 2 \, q^{7} t - 6 \, q^{6} t - q^{5} t^{2} + q^{4} t + 6 \, q^{3} t^{2} - 2 \, q^{2} t^{2} - t^{3}}{{\left(q^{2} - t\right)}^{2} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
7 edges: [[0, 3], [0, 4], [1, 2], [1, 4], [2, 3], [2, 4], [3, 4]]

[0045] 'DNw'

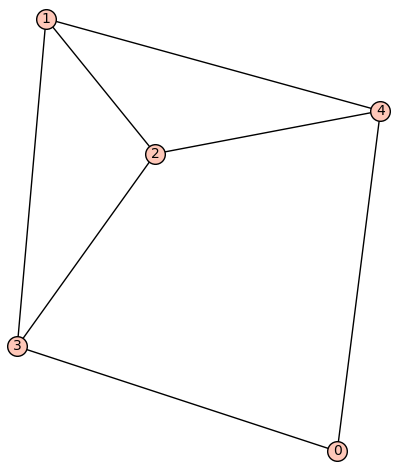
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{10} + q^{8} t - q^{7} t - 6 \, q^{6} t - 3 \, q^{5} t^{2} + 3 \, q^{5} t + 6 \, q^{4} t^{2} + q^{3} t^{2} - q^{2} t^{2} - t^{3}}{{\left(q^{3} - t\right)} {\left(q^{2} - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
7 edges: [[0, 3], [0, 4], [1, 2], [1, 3], [1, 4], [2, 3], [2, 4]]

[0046] 'DN{'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{7} + q^{5} t - 2 \, q^{4} t - 2 \, q^{3} t + q^{2} t + t^{2}}{{\left(q^{2} - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
8 edges: [[0, 3], [0, 4], [1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

[0047] 'D]{'

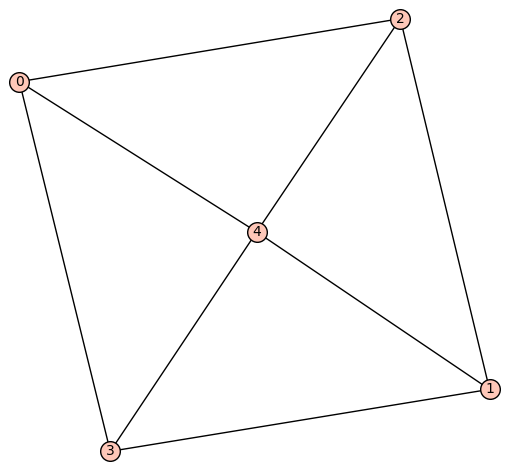
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{8} + 3 \, q^{5} t - 8 \, q^{4} t + 3 \, q^{3} t + t^{2}}{{\left(q^{3} - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
8 edges: [[0, 2], [0, 3], [0, 4], [1, 2], [1, 3], [1, 4], [2, 4], [3, 4]]

[0048] 'D^{'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{8} + q^{5} t - 4 \, q^{4} t + q^{3} t + t^{2}}{{\left(q^{3} - t\right)} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
9 edges: [[0, 2], [0, 3], [0, 4], [1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

[0049] 'D_K'

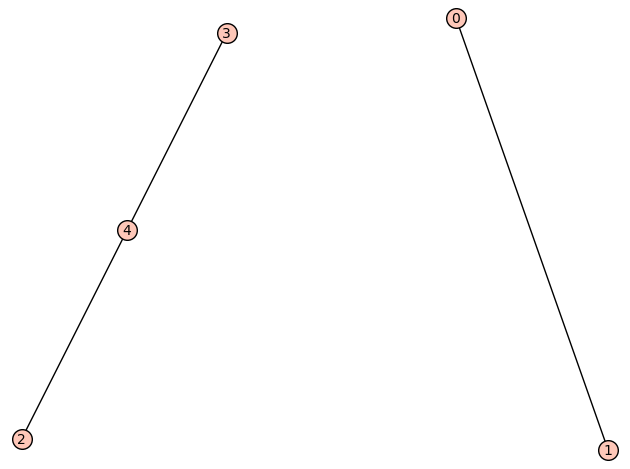
Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{7} t - 2 \, q^{6} t^{2} - q^{5} t^{3} + q^{7} + 2 \, q^{6} t - q^{5} t^{2} + 4 \, q^{4} t^{3} - 10 \, q^{5} t + 6 \, q^{4} t^{2} + 6 \, q^{3} t^{2} - 10 \, q^{2} t^{3} + 4 \, q^{3} t - q^{2} t^{2} + 2 \, q t^{3} + t^{4} - q^{2} t - 2 \, q t^{2} + t^{3}}{{\left(q - t\right)}^{2} q^{5} {\left(t - 1\right)}^{3}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
3 edges: [[0, 1], [2, 4], [3, 4]]

[0050] 'D`K'

Plot of graph
Zeta functions
ask[#]: \(\displaystyle -\frac{q^{5} t + q^{5} - 2 \, q^{3} t - 2 \, q^{2} t + t^{2} + t}{q^{5} {\left(t - 1\right)}^{3}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
4 edges: [[0, 1], [2, 3], [2, 4], [3, 4]]

[0051] 'Dbk'

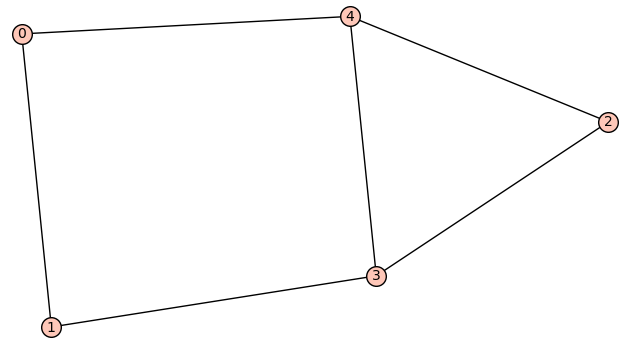
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{9} + 4 \, q^{7} t - 10 \, q^{6} t - q^{5} t^{2} + 2 \, q^{5} t - 2 \, q^{4} t^{2} + q^{4} t + 10 \, q^{3} t^{2} - 4 \, q^{2} t^{2} - t^{3}}{{\left(q^{2} - t\right)}^{2} q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
6 edges: [[0, 1], [0, 4], [1, 3], [2, 3], [2, 4], [3, 4]]

[0052] 'D~{'

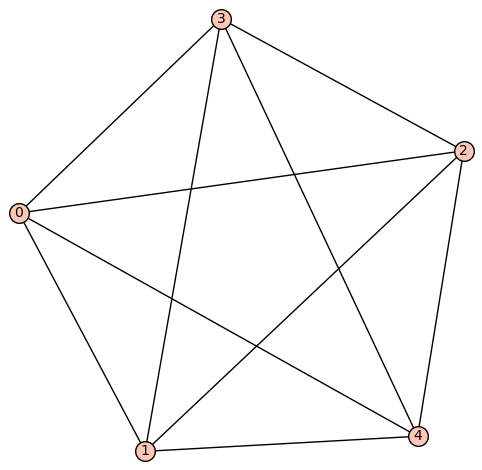
Plot of graph
Zeta functions
ask[#]: \(\displaystyle \frac{q^{5} - t}{q^{5} {\left(t - 1\right)}^{2}}\)
Graph:
5 vertices: [0, 1, 2, 3, 4]
10 edges: [[0, 1], [0, 2], [0, 3], [0, 4], [1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]
Created: 2025-05-13 16:45:50.464775+00:00